Robust design optimization and robust optimal control
Introduction
Practical application of the numerical optimization results is
difficult because of the fact that any complex technical system is a stochastic system
and the characteristics of this system have probabilistic nature. We would
like to emphasize that, speaking about the stochastic properties of
a technical system within the frame of optimization tasks, we imply that
the important parameters of any
system are stochastically spread. Normally it occurs during the production
stage despite of the up-to-date level of modern technology. Random
deviations of the system parameters lead to a random change in system efficiency.
An efficiency extreme value, obtained during the optimization problem
while solving in traditional (deterministic) approach, is simply a
maximum attainable value and can be considered as just conventional
optimum from the point of view of its practical realization. Thus, one
can consider two different types of optimization criteria. One of them
is an ideal efficiency which can be achieved under the conditions of
absolutely precise practical replication of the system parameters under
consideration. Other optimization criteria are of probabilistic nature. For example:
mathematical expectation of the efficiency; the total probability of assuring
preset constraints; variance of the efficiency and so on
It is evident that the extreme of the one of these criteria doesn't guarantee
the assurance of the high level of another one. Even more, these criteria
may contradict to each other. Thus, in this case we have a multicriteria
optimization problem.
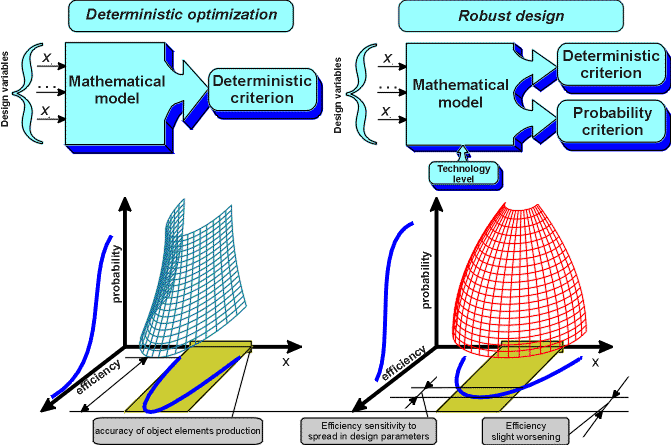
Our concept
Our concept of robust design optimization and robust optimal control
allows to determine the optimal practical solution that could
be implemented with the high probability for the given technology level
of the production plants. Many modern probabilistic approaches either
employ the estimation of probabilistic efficiency criteria only at the stage
of the analysis of obtaining deterministic solution, or use significantly
simplified assessments of probabilistic criteria during optimization process.
The distinctive feature of our approach is that during robust design optimization
we solve the optimization problem involving direct stochastic formulation,
where the estimation of probabilistic criteria is accomplished at each iteration.
This procedure reliably produces fully robust optimal solution. High efficiency
of the robust design optimization is provided by the capabilities of IOSO
algorithms to solve stochastic optimization problems with large level
of noise.
Our robust design optimization concept provides considerable (several
orders of magnitude) reduction in cost and time during the development of
the new highly efficient systems. This concept also considerably (several
times) reduces risk associated with new technical solutions.
For example,
during optimal calibration of the automotive engine the development time
was reduced by 5 times, during development of the new axial compressor
more than 200 times. The most important feature of IOSO technology is
the ability to solve robust design optimization problems with the large
number of variables (hundreds) and efficiency criteria (dozens).
Real-life example
MULTICRITERIA ROBUST DESIGN OF THE MULTISTAGE AXIAL FLOW COMPRESSOR
Problem features: 140 design variables, 2 criteria.
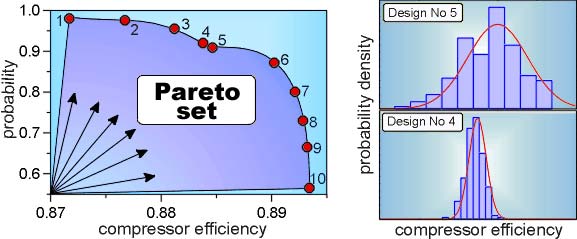
The trade-off area:
the compressor efficiency grows from 0.87 up to 0.89
while
the implementation probability reduces from 0.97 down to 0.56 !
The solution N1 could be implemented with high probability, but it
has low efficiency. Solution N10 has high efficiency, but has the low
probability of practical implementation. The solutions N4 and N5 have
very similar efficiencies and probability of implementation, but N4 is
better, because it has lower level of efficiency distribution. It is the
solution (N4) that should be implemented in practice.
Back...
| 