MDO concept in details

A general view of such a concept is presented in Figure below. The attempt to take into account all possible optimization problem statements resulted in the scheme where a system under study is shown as a certain cube with a large number of layers, each corresponding to a separate engineering discipline. Within the frameworks of each discipline, system analysis can be performed using different tools from the simplest mathematical models to possible prototype experimental evaluations.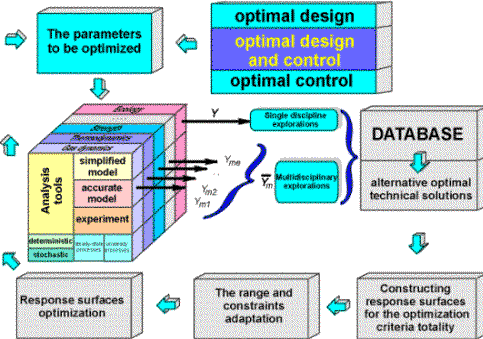

The structure of the proposed multidisciplinary optimization concept

Our MDO approach is based on the response surface technique and on the original approximation concept. Within the framework of these concept we adaptively use global and middle-range approximations. One of the advantages of the proposed approach is the possibility of ensuring good approximating properties using minimum amount of available information. This is also ensured by application of self-organization and evolutionary modeling concepts. During the optimization process, the approximation function structure is evolutionarily changed, so that we are able to successfully approximate the objective functions and constraints of complicated topology.

The obtained response surface functions can be naturally used by multilevel optimization procedures with the adaptive change of simulation level for both single and multi-disciplinary analysis. These response surface could also be used for interconnection problems solution when solving multidisciplinary optimization problems.

Solution of multicriteria optimization problems is based on the use of response surfaces for individual objectives and constraints. Another part of our strategy is adaptive change of the current search area. This adaptive change makes it possible to search for the Pareto-optimal set without applying convolution approaches. The use of multicriteria optimization algorithms allows us to integrate different disciplines into the united computational process. The given approach is the main one for overcoming the so-called organizing difficulties in MDO traditional concepts.

Example

(Optimization of the controllable axial compressor)

One of the problem that inevitably arises while optimizing the aircraft compressor, is to ensure high performance not only for one condition (design point), but over the entire operating range. The variables, characterizing a compressor can be divided into two groups. The first group of variables (design variables) contains the characteristics that do not vary when the operating mode is changed. The second group comprises the control variables which can be purposefully changed. The presence of the functional variables that can be purposefully varied suggests the solution of an optimal control problem.

We conventionally define three kinds of the optimization problems related to the development of an "optimum" compressor.

1. Optimum design problem. The goal of this problem is to determine the optimal design variables; the values of these variables are independent from the operating mode.

2. Optimum control problem. The goal of this problem is for the given and immutable variables of the first group find the optimal control law for the variables of the second group for all operating modes.

3. Optimum design-and-control problem. The goal of this problem is to simultaneously determine the optimal values of the design variables and the control laws.

The third problem seems to be the most promising, since it allows us to take into consideration the interdependency between the compressor design and its controllability. The solution of this problem allows us to implement the design and control features in the most comprehensive way. The third problem is also a typical example of the MDO problem.

In this example the initial compressor's project had been obtained "by hand" (without use of optimization methods); the optimal designing of uncontrollable compressor had been carried out by criterion of efficiency maximum at design-point operating mode (n_rc=1.0); then for this project the optimal control problem had been solved (the criterion was compressors efficiency at n_rc=0.8); the simultaneous optimization of both design parameters and control laws had been carried out for two operating modes.

1. Initial design 2. Optimum design of uncontrollable compressor 3. Optimum control with fixed geometry, based upon results of optimum design of uncontrollable compressor 4. Optimum design of controllable compressor

Compressor efficiency increments attainable through various optimization problems

Back...

© Sigma Technology 2001.