IOSO NS GT v.2.0 is the program package implementing IOSO Technology algorithms for a single-objective nonlinear optimization with a moderate number of design variables (up to 100). The program is intended for Windows 98, NT4.0, ME,  2000, XP operating systems.

Distinctive features of IOSO NS GT 2.0:

High efficiency of the evolutionary self-organizing algorithm. The efficiency is guaranteed by internal adaptive choice of the algorithm suitable for each particular problem. This feature results in solving complex optimization problems with minimal number of evaluations of the system mathematical model.

1. Universality of the optimization procedure. The program could be equally efficiently used to solve problems with smooth objective function and constraints as well as problems with non-differentiable, “noisy’, multiextremum objective function and constraints that could potentially have the regions where objective function and constraints could not be evaluated. We may state with confidence, that currently there exist no optimization packages with the same set of capabilities. Particularly when comparing efficiency of the packages for a wide range of real-life problems.

2. User friendly GUI and simplicity of use. Most of the algorithm tunings are done internally and are hidden from the user. The user does not have to know practically anything about nonlinear programming and optimization. The only important thing for the user is to understand the physics of the problem and to have a mathematical model of the system.

3. Creating an interface between our program and mathematical model typically takes just several minutes. Mathematical model should be represented by an executable file prepared by the user. The data exchange between mathematical model and our package is accomplished through files with design variables, objective function, and constraints.

4. Visual real-time representation of the optimization process (current values of the design variables and their bounds, objective function history).

5. User’s ability to control optimization process (interruption of the optimization process to tune up parameters with ability to restart from the specified point, cleaning up “hanged” or crashed user’s mathematical model).

In general, executable module with user’s mathematical model should be able to perform the following sequence of operations:

1. Read the file with the values of the design variables in free format.

2.  Calculation of the objective function and constraints values.

3. Writing out objective function and constraints values into the file in free format.

To set up an optimization problem the user has to do the following:

1. Define the direction of optimization search (minimize or maximize).

2. Define the number of design variables and their bounds.

3. Define the constraints,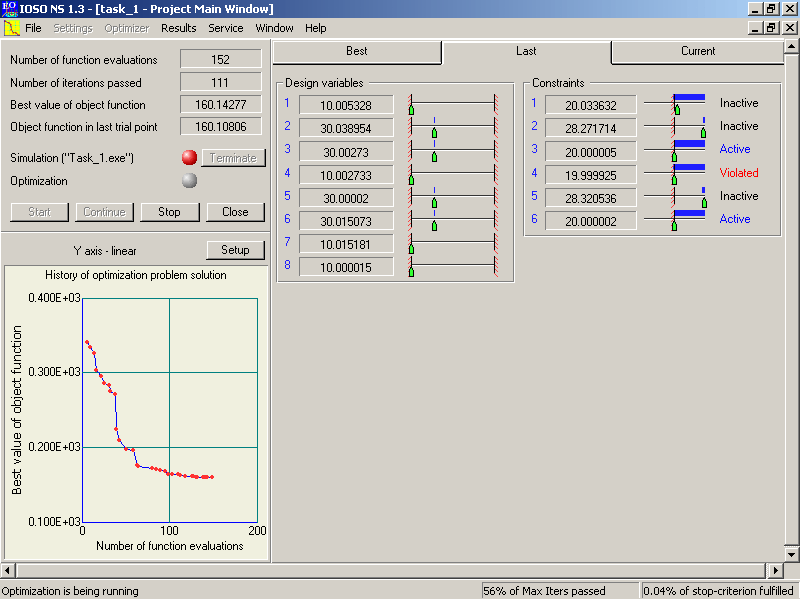 the numerical values for the constraint bounds and the type of constraint (less than or greater than).

4. Define the maximum number of iteration and the required precision of the final solution (with what precision the constraints should be satisfied at the optimum).

5. Specify the name of the executable with mathematical model (if necessary, the command line invoking mathematical model could be provided), the name of the files with the design variables, and the name of the file with objective function and constraints.

6.  Start the optimization process .