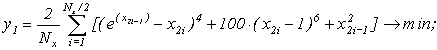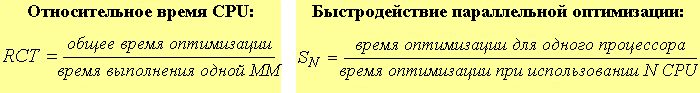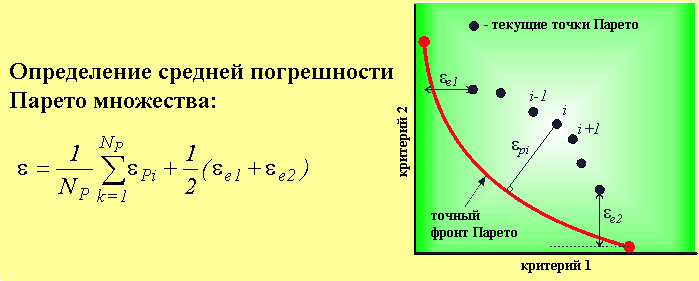
The analytical determination of the Pareto set for the given test is extremely difficult. The "exact" solution has been obtained by means of the detailed scanning of variable parameters space (the scanning interval had the value of 10^-4) for N_x=2. It is easy to realize that the increase of the optimization problem dimensionality (N_x=4,6,8,) would not lead to the "exact" solution change.

It must be noted that when using traditional approach to the analysis of parallelization computation efficiency the ideal value of this index is equal to the number of the applied processors (S_N=N). However, for the parallel optimization algorithm, the change of the number of processors being used corrects the information volume which is being analyzed when going from one iteration to another. Thus, in our case the effectiveness of computations parallelization (S_N /N) can be both less and more than 1.

This figure shows an example of S_N parameter variation demonstrating the high parallelized computations efficiency. One can see that for the considered test conditions the S_N parameter value exceeds the total number of operational CPUs. It proves that this parallel optimization algorithm has the higher "internal" efficiency than one of IOSO basic (single-CPU) version. It also proves that the given optimization procedure has been developed according to the parallel optimization process, and that it does not represent a trivial usage of several CPUs for the solution of optimization problems.