|
|
|
| |
| |
Оптимизация и оптимальное управление
при наличии неопределенностей
|
Введение
|
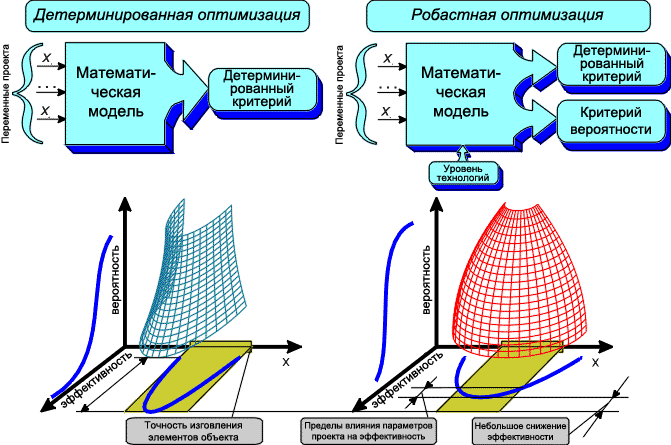
Practical application of the numerical optimization results is complicated by the fact that any intricate technical system is a stochastic system and characteristics of this system have a probabilistic nature. We would like to emphasize the point that, speaking of stochastic properties of a technical system within the frame of optimization tasks, we imply a system's essential parameters spread which occurs during the production stage despite the up-to-date level of technology. Random deviations of the system's parameters lead to a random change in system's efficiency.
An efficiency extremum value, obtained during the optimization problem solving in a traditional (deterministic) setting, is simply a maximum attainable value and can be considered as just conventional optimum from the point of view of its practical realization. Thus, one can consider two different types of optimization criteria. One of them is an ideal efficiency which can be achieved under the conditions of absolutely precise practical replication of the preset parameters of the system under consideration. Other optimization criteria are of probabilistic nature. For example: mathematical expectation of the efficiency; total probability of assuring the preset constraints; variance of the efficiency and so on.
It is evident that the extremum of one of these criteria doesn't guarantee the assurance of the high level of another one. Even more, these criteria may be contradicting each other. Thus, in this case we have a multicriteria optimization problem. |
|
| |
|
| |
| |
Наша концепция
|
Наша концепция оптимизации и оптимального управления при наличии неопределенностей позволяет определять оптимальные технические решения, реализуемые на практике с высокой вероятностью, для заданного уровня технологии производства. Известны подходы, когда оценка вероятностных критериев эффективности осуществляется либо лишь только на этапе анализа полученного детерминированного решения, либо используются сильно упрощенные оценки вероятностных критериев в процессе оптимизации. Отличительная особенность нашей концепции заключается в том, при оптимизации при наличии неопределенностей осуществляется решение задачи оптимизации непосредственно в стохастической постановке, когда на каждой итерации поиска решения осуществляется оценка вероятностных критериев. Это обеспечивает надежное определение действительно робастного оптимального решения. Высокая эффективность решения задачи оптимизации при наличии неопределенностей обеспечивается возможностями алгоритмов IOSO по решению задач стохастической оптимизации при больших уровнях помех.
Использование нашей концепции оптимизации при наличии неопределенностей обеспечивает значительное снижение затрат и сроков (на несколько порядков) при разработке новых высокоэффективных технических объектов, а также существенно (в несколько раз) уменьшает степень риска при принятии новых технических решений. Так, при оптимальной калибровке автомобильного двигателя на стенде временные затраты были снижены в 5 раз, при разработке проекта нового осевого компрессора, – более чем в 200 раз. Важнейшей отличительной особенностью IOSO технологии является возможность решения проблем оптимизации при наличии неопределенностей с большим числом проектных параметров (сотни переменных) и критериев эффективности (десятки целевых функций). |
|
| |
| |
Пример реальной жизни
|
МНОГОКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ С НАЛИЧИЕМ НЕОПРЕДЕЛЕННОСТЕЙ ПРИ
ПРОЕКТИРОВАНИИ
МНОГОСТУПЕНЧАТОГО ОСЕВОГО ПОТОЧНОГО КОМПРЕССОРА |
| |
Прикладные особенности: 140 проектных переменных, 2 критерия.
|
|
| |
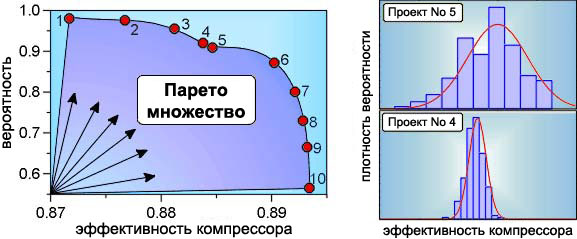
Область компромисса:
|
эффективность компрессора от 0.87 до 0.89 с вероятностью реализации от 0.97 и ниже до 0.56!
|
The solution N1 could be implemented with a high probability, but it has low efficiency. Solution N10 has a high efficiency, but has a low probability of practical implementation. The solutions N4 and N5 have very similar efficiencies and probability of implementation, but N4 is better, because it has lower level of efficiency distribution. It is this solution (N4) that should be implemented in practice. |
|
| |
| |
|
|
|